Stephen R. Green
UKRI Future Leaders Fellow
University of Nottingham -- School of Mathematical Sciences
Biography
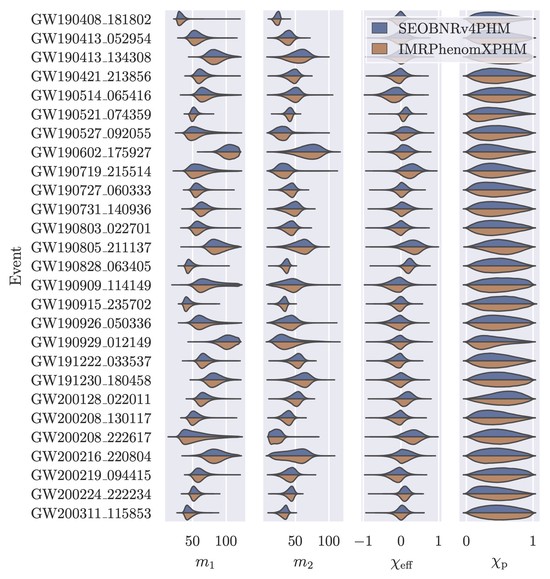
I am a researcher in gravitational waves at the University of Nottingham in the School of Mathematical Sciences. My current interests are in black hole perturbation theory and machine-learning methods for data analysis. I was recently awarded a UKRI Future Leaders Fellowship to develop AI / simulation-based inference methods for gravitational waves.
I grew up in Toronto, Canada, where I attended the University of Toronto. I obtained my PhD in physics at the University of Chicago under Robert Wald, where I studied effects of general relativity in cosmology and debunked the idea that small scale structure could drive cosmological acceleration and mimic dark energy. I then moved to the University of Guelph and Perimeter Institute, where I studied turbulence in gravitational waves and black hole superradiant instabilities. I then spent five years at the Albert Einstein Institute in Potsdam, where I became a member of LIGO and worked on gravitational waves.
Interests
- Gravitational Waves
- Black Holes
- Machine Learning
Education
PhD in Physics, 2012
University of Chicago
SM in Physical Sciences, 2006
University of Chicago
BSc in Mathematics and Physics, 2005
University of Toronto