Spacetime Turbulence

In standard astrophysical contexts, gravitational waves propagate away from a source at the speed of light. But in some special geometries, waves are confined and cannot escape. This gives them time to grow through nonlinear interactions.

Spacetime turbulence

When large black holes in anti-de Sitter spacetime are perturbed, they ring down very slowly, i.e., they have long-lived quasinormal modes. This gravitational ringdown has been identified with the hydrodynamic modes of a fluid in one lower dimension, which gave rise to the “gravity/fluid correspondence.” Fluids can develop turbulence, so I became interested in the question of whether this can happen in the dual spacetime?

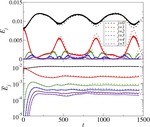
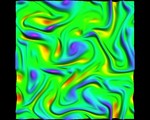
With F. Carrasco and L. Lehner, we studied this ringdown numerically by exploiting this correspondence between the spacetime metric and the fluid. We considered a relativistic viscous fluid living in $(2+1)$-dimensional flat spacetime, which is dual to a black hole in $3+1$ dimensions. We showed that under evolution, the fluid develops turbulent vortices and eddies, and that there are dual cascades of energy and enstrophy. We extrapolated these results into the black hole spacetime and we verified that they matched direct gravitational studies.

Instability of anti-de Sitter

Next, with A. Buchel, L. Lehner, and S. Liebling, we studied perturbations of global anti-de Sitter spacetime. This spacetime is completely confining—there is no dissipation—and had been conjectured to be unstable. Numerical evidence also showed that tiny perturbations would grow through nonlinear interactions to become very large, eventually forming a black hole . The question is whether arbitrarily small perturbations always collapse? Are there special perturbations that don’t?

These questions cannot be addressed through numerical simulations, so we applied two-timescale perturbation theory: we found a way to “average” out typical wave oscillations, and analyze separately the nonlinear energy flows between wave modes. Using this, we found surprising connections between the AdS stability problem and the old Fermi-Pasta-Ulam-Tsingou problem of ergodic versus periodic behavior for nonlinearly coupled harmonic oscillators.

Applying techniques from nonlinear dynamics, we identified a new approximate conservation law for this system (“wave action”) and we showed that there exist “islands of stability” where initial data do not appear to lead to collapse.